Allgemeine Form

$$\begin{align}f(t)=S+\big(f(0)-S\big)e^{-kt}\end{align}$$​​
Das ist die allgemeine Form des begrenzten Wachstums.
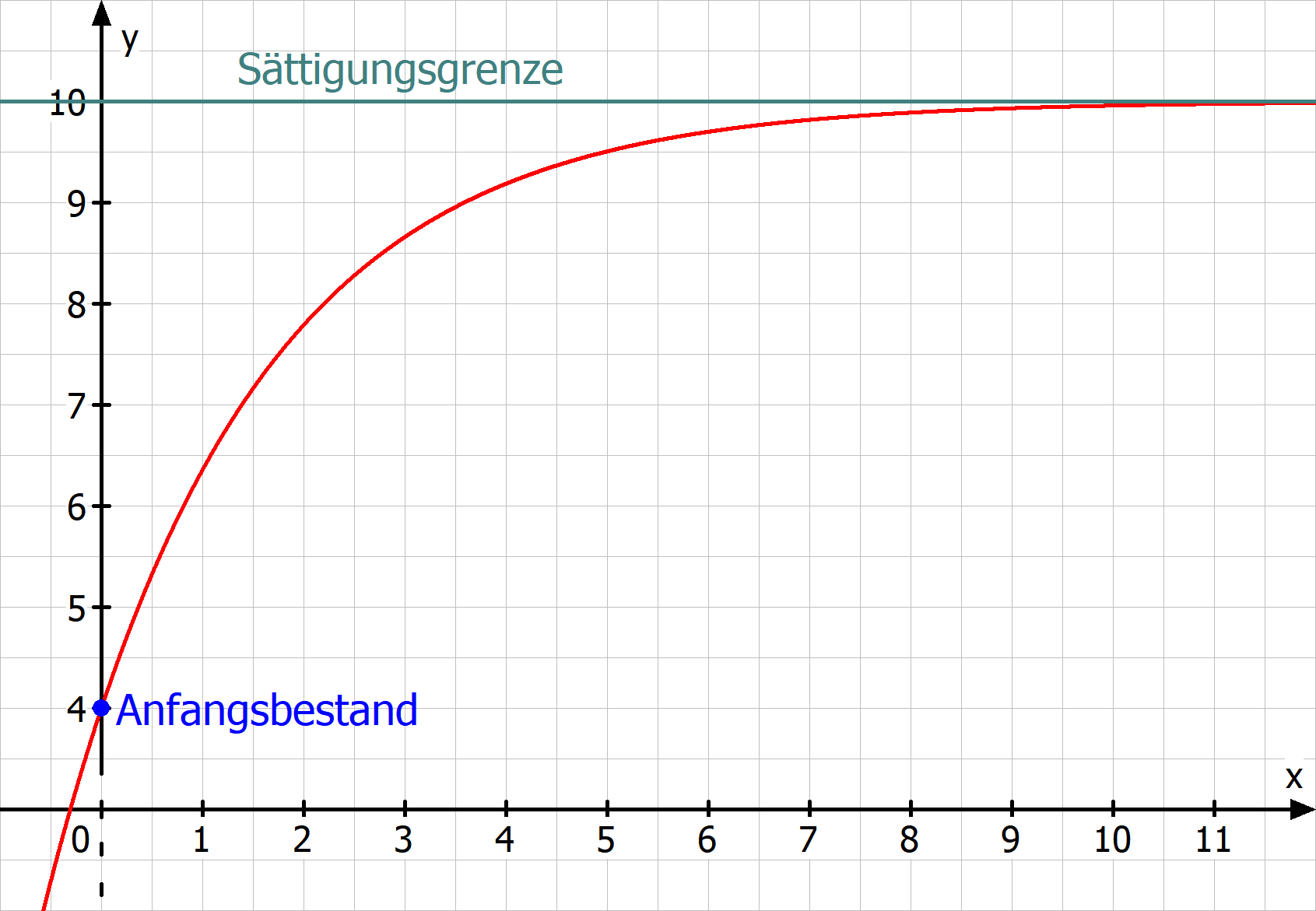
- $S$ ist die Sättigungsgrenze, welche die Asymptote markiert. Also eine Funktion, die sich der des begrenztes Wachstum annähert. So wird in dem Beispiel unten die Funktion niemals y=10 erreichen. Sie nähert sich eben an.
- $f(0)$ ist der Anfangsbestand
- $k$ ist der Wachstumsfaktor der bestimmt, wie schnell sich die Funktion der Sättigungsgrenze annähert.

Dazugehörige Funktionsgleichung:
$$\begin{align}f(x)=10+(4-10)e^{-0,5x}\end{align}$$

Wann Wachstum, wann Zerfall?
Wenn die Funktion nach dem Wert für die Sättigungsgrenze ein positives Vorzeichen aufweist, dann ist es ein begrenzter Zerfall, wenn das Vorzeichen negativ ist, ein begrenztes Wachstum.
 $$\begin{align} 70{\color{OliveGreen}{+}}50\cdot e^{-0,2x} \Longrightarrow \text{begrenztes Zerfall} \\ \\ 10+(4-10)\cdot e^{-0,5} \Longrightarrow 10{\color{OliveGreen}{-}}6\cdot e^{-0,5} \Longrightarrow \text{begrenztes Wachstum} \end{align}$$