Abstand zwischen Punkt und Gerade

Aufgabenstellung
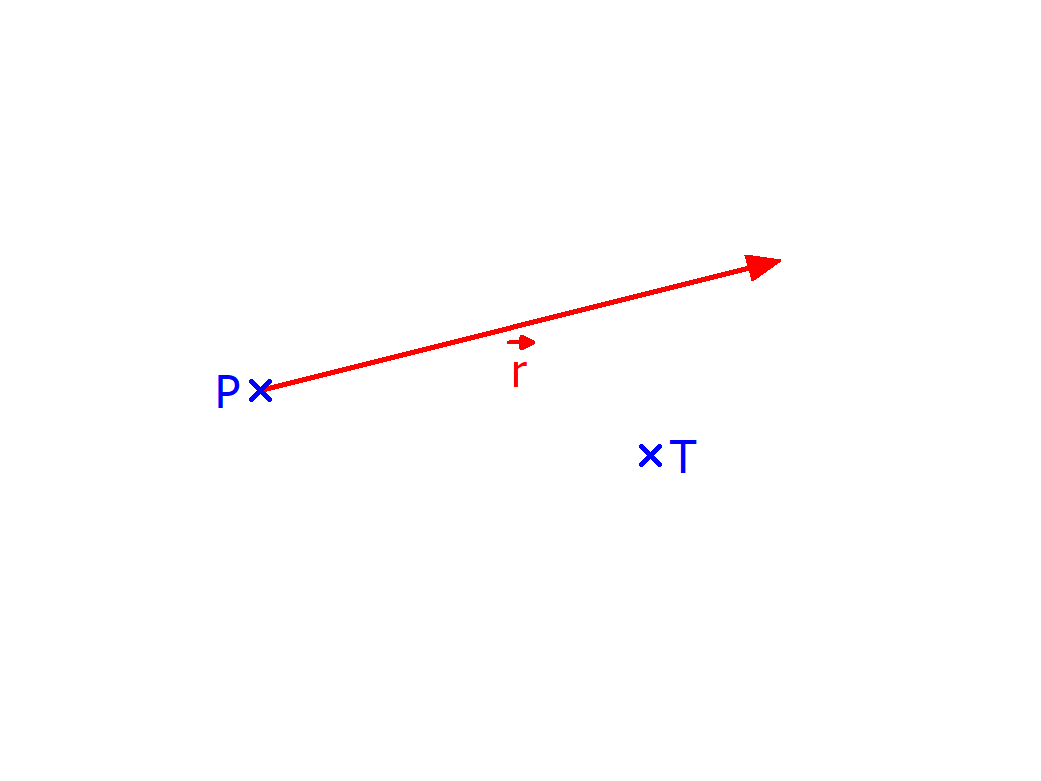
Nils spielt Fußball. Ausversehen schießt er einen Ball so, dass er knapp an Donald Trumps Kopf vorbeifliegt. Donald Trump ist sehr erbost über diesen "Anschlag" und fordert ein genaues Gutachten, wie knapp der Ball seinen Kopf verfehlt hat. Nun wurdest du darum gebeten, diese Analyse durchzuführen. Durch Auswertung der Überwachungskameras konnte festgestellt werden, dass der Ball von dem Punkt $P(1|2|0)$ aus in Richtung $\vec{r}=\left(\begin{array}{c} 4 \\ 1 \\ 0 \end{array}\right)$ von Nils geschossen wurde. Donald Trumps Kopf befand sich bei dem Punkt $T(4|1,5|0)$. 

Das ganze sieht Graphisch so aus:

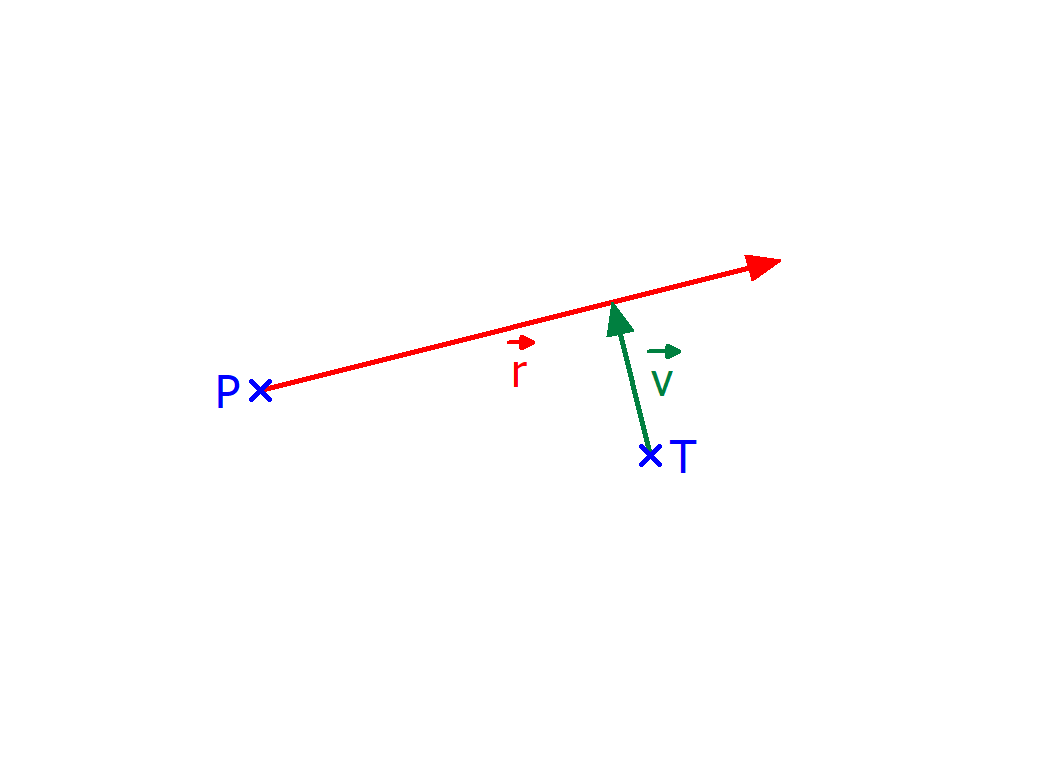
Wir sollen ja die kürzeste Distanz zwischen der Gerade und dem Punkt herausfinden. Dieser Punkt befindet sich genau dort, wo der Verbindungsvektor ($\vec{v})$ zwischen $T$ und der Gerade rechtwinklig ist. Hier noch einmal visuell:

Und das ganze kann man mit dem Skalarprodukt prüfen, denn nur wenn die Gerade und der Verbindungsvektor $\vec{v}$ rechtwinklig verlaufen, dann ergibt das Skalarprodukt aus beiden Vektoren Null.

Verbindungsvektor $\vec{v}$ errechnen:

Nun kann man im ersten Schritt den Verbindungsvektor von $T$ nach $P$ bestimmen:
$$\overrightarrow{TP}=\vec{P}-\vec{T}=\left(\begin{array}{c} -3 \\ 0,5 \\ 0 \end{array}\right)$$

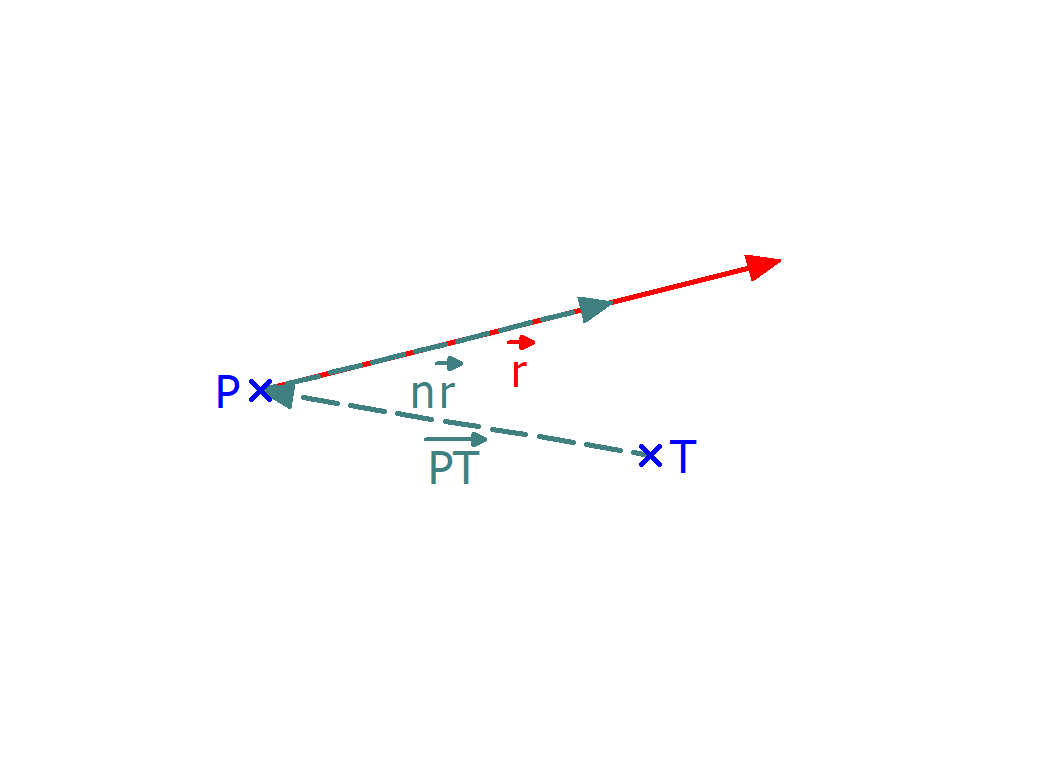
Um nun zu dem Punkt zu gelangen, an dem $\vec{v}$ rechtwinklig zu der Gerade ist, muss man einfach nur folgendes machen:
$$\begin{align}\vec{v}&=\overrightarrow{TP}+n\cdot \vec{r} \\ \\\vec{v}&=\left(\begin{array}{c} -3 \\ 0,5 \\ 0 \end{array}\right)+n\cdot \left(\begin{array}{c} 4 \\ 1 \\ 0 \end{array}\right)\end{align}$$
Das sieht jetzt erst einmal komisch aus, aber es beschreibt tatsächlich den Vektor $\vec{v}$:

Man muss eben von $T$ nach $P$ und dann von dort aus $n$ mal in Richtung des Richtungsvektors gehen. 

Darstellungsweise von $\vec{v}$
Durch zusammenfassen kann $\vec{v}$ auch so aussehen:$$
\vec{v}=\left(\begin{array}{c} -3+4n \\ 0,5+1n \\ 0 \end{array}\right)$$

Skalarprodukt aufstellen:

 $$\begin{align}\vec{v}\cdot \vec{r}&=0 \\ \\\left(\begin{array}{c} -3+4n \\ 0,5+1n \\ 0 \end{array}\right)\cdot \left(\begin{array}{c} 4 \\ 1\\ 0 \end{array}\right) &=0\end{align}$$
Jetzt muss man nur noch $n$ ausrechnen:
$$\begin{align}(-3+4n)\cdot 4+(0,5+1n)\cdot 1+0\cdot 0&=0 \\-12+16n+0,5+n&=0 \\-11,5+17n&=0 &&|+11,5 \\17n&=11,5 &&|\div{17} \\n&=\frac{23}{34}\end{align}$$
Nun kann man $n$ einfach in den Vektor $\vec{v}$ einsetzen und ausrechnen, welcher Vektor die kürzeste Distanz zwischen dem Ball und Trumps Kopf beschreibt.
$$n\text{ in }\vec{v}:\left(\begin{array}{c} -0,29 \\ 1,18 \\ 0 \end{array}\right)$$
Jetzt kann man noch die Länge ausrechnen und weiß, wie knapp der Ball an Kopf von Trump vorbeigeflogen ist:
$$|\vec{v}|=\sqrt{(-0,29)^{2}+1,18^{2}+0^{2}}=1,22$$
Das bedeutet, der Ball ist dramatische 1,22$m$ "knapp" an Trumps Kopf vorbeigeflogen.