Zwischen zwei parallelen Ebenen
Aufgabenstellung
Gegeben ist die Ebene $E_{1}: x-2y-2z=2$ und die Ebene $E_{2}: -3x+6y+6z=21$. Berechnen Sie den Abstand zwischen Ihnen.
Hier eine Skizze: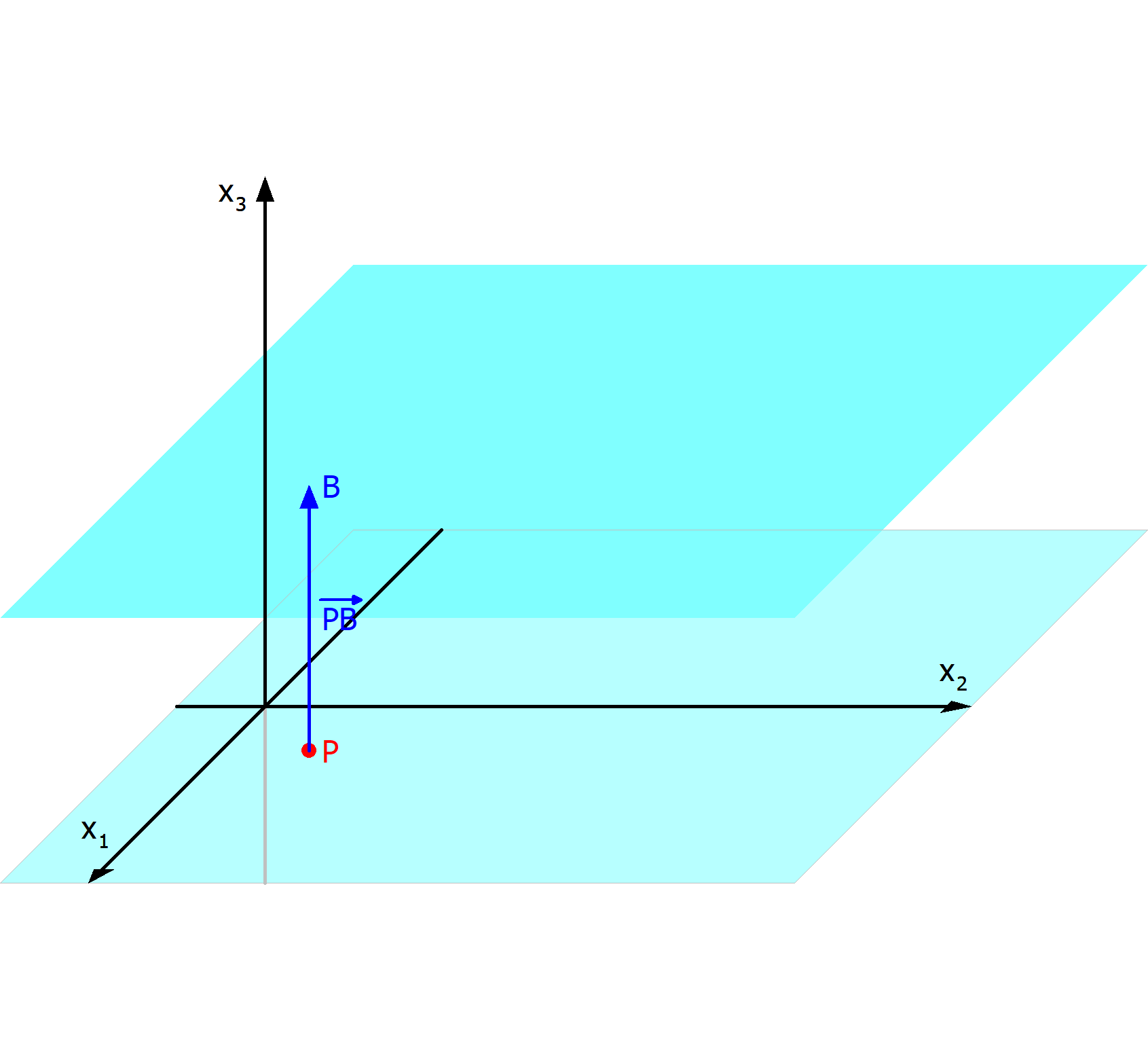 Der erste Schritt um den Abstand zwischen zwei parallelen Ebenen zu berechnen ist es, einen Punkt auf einer Ebene ausfindig zu machen. Das geht durch das logische ausfüllen einer Gleichung:
Der erste Schritt um den Abstand zwischen zwei parallelen Ebenen zu berechnen ist es, einen Punkt auf einer Ebene ausfindig zu machen. Das geht durch das logische ausfüllen einer Gleichung:
$$E_{1}: x-2y-2z=2$$
Angenommen $y=0$ und $z=0$, dann müsste $x=2$ sein damit die Gleichung aufgeht. So hat man einen Punkt auf der Ebene 1 gefunden: $P(2|0|0)$.
Nun kann man den Punkt mit dem Normalenvektor der Gerade zu einer Geradengleichung zusammenfügen, da man bei der Koordinatenform einer Ebene den Normalenvektor herauslesen kann.
$$\begin{align}\vec{g}&=\left(\begin{array}{c} 2 \\ 0 \\ 0 \end{array}\right)+r\cdot \left(\begin{array}{c} 1 \\ -2 \\ -2 \end{array}\right)\end{align}$$
Der Vektor beschreibt eine Gerade von dem Punkt $P$ aus in Richtung des Normalvektors. Da so eine Rechtwinklige Gerade zwischen den Ebenen ensteht, kann man einfach errechnen, wo sich die Gerade mit der Ebene 2 trifft:
$$\begin{align}\vec{g}\text{ in }E_{2}:\quad -3\cdot (2+r)+6\cdot (-2r)+6(-2r)&=21 \\
-6-3r-12r-12r&=21 \\-6-27r&=21 &&|+6 \\-27r&=27 &&|\div(-27) \\r&=-1\end{align}$$
Das bedeutet wenn man $r$ in die Geradengleichung eingibt, trifft man mit ihr auf die Ebene 2:
$$\begin{align}r\text{ in }\vec{g}:&\quad \left(\begin{array}{c} 2 \\ 0 \\ 0 \end{array}\right)+(-1)\cdot \left(\begin{array}{c} 1 \\ -2 \\ -2 \end{array}\right) \\ \\r\text{ in }\vec{g}:&\quad \left(\begin{array}{c} 1 \\ 2 \\ 2 \end{array}\right)\end{align}$$
Nun kennt man den Punkt $B(1|2|2)$, bei dem die Geradengleichung die Ebene 2 schneidet.
Damit kann man dann auch den Abstand zwischen den Punkten $P$ und $B$ berechnen:
$$\begin{align}\vec{v}&=\overrightarrow{PB}=\left(\begin{array}{c} 1 \\ 2 \\ 2 \end{array}\right)-\left(\begin{array}{c} 2 \\ 0 \\ 0\end{array}\right)=\left(\begin{array}{c} -1 \\ 2 \\ 2 \end{array}\right) \\ \\|\vec{v}|&=\sqrt{(-1)^{2}+2^{2}+2^{2}} \\|\vec{v}|&=3\end{align}$$
Der Abstand zwischen den Punkten beträgt 3 Längeneinheiten.
$$
\begin{alignat}{3}
\text{I:}&\quad
\begin{alignat}{2}&2n_{1}+4n_{3}&=0 x &+ y &= 10 \\
\text{II:}&\quad &3n_{1}+2n_{2}+2n_{3}&=0 2x\\ \\
\text{I:}&\quad &2n_{1}+4n_{3}&=0\\
-1\cdot\text{II:}&\quad y&\underline{-3n_{1}-2n_{2}-2n_{3}}&=\underline{0}\\
\text{III:}&\quad &-n_{1}-2n_{2}+2n_{3}&=0 3\\ \\
3\cdot\text{III:}&\quad &-3n_{1}-6n_{2}+6n_{3}&=0 \end{alignat\
\text{II:}
&\underline{3n_{1}+2n_{2}+2n_{3}}&=\underline{0} \\
\text{IV:}&\quad &-4n_{2}+8n_{3}&=0 \quad\quad|\text{Sei }n_{3}=1 \\
&&-4n_{2}+8&=0\quad\quad|-8 \\
&&-4n_{2}&=-8\ \quad|\div{(-4)} \\
&&n_{2}&=2 \\ \\
n_{2}\text{ in IV:}&\quad &-4\cdot 2+8n_{3}&=0\quad\quad|+8 \\
&&8n_{3}&=8\quad\quad|\div{8}\\
&&n_{3}&=1 \\ \\
n_{3}\text{ in I:}&\quad&2n_{1}+4&=0\quad\quad|-4 \\
&&2n_{1}&=-4\ \quad|\div{2} \\
&&n_{1}&=-2
\end{alignat}
$$
