Zwischen Punkt und Ebene (Lotfußpunktverfahren)
Der Name "Lotfußpunktverfahren" klingt zwar so, als hätte der Erfinder einen Schlaganfall gehabt (Ironie), es ist allerdings eine sehr gute Methode um den Abstand zwischen einem Punkt und einer Ebene herauszufinden.
Aufgabenstellung
Berechnen Sie den Abstand zwischen der Ebene $E:z=0$ und dem Punkt $A(2|4|3)$.
Hier ist eine kleine Skizze unserer Situation. Man sieht den Punkt $A$ in rot und die Ebene in Türkis. In blau ist der Abstand zwischen ihnen als Verbindungsvektor eingezeichnet.
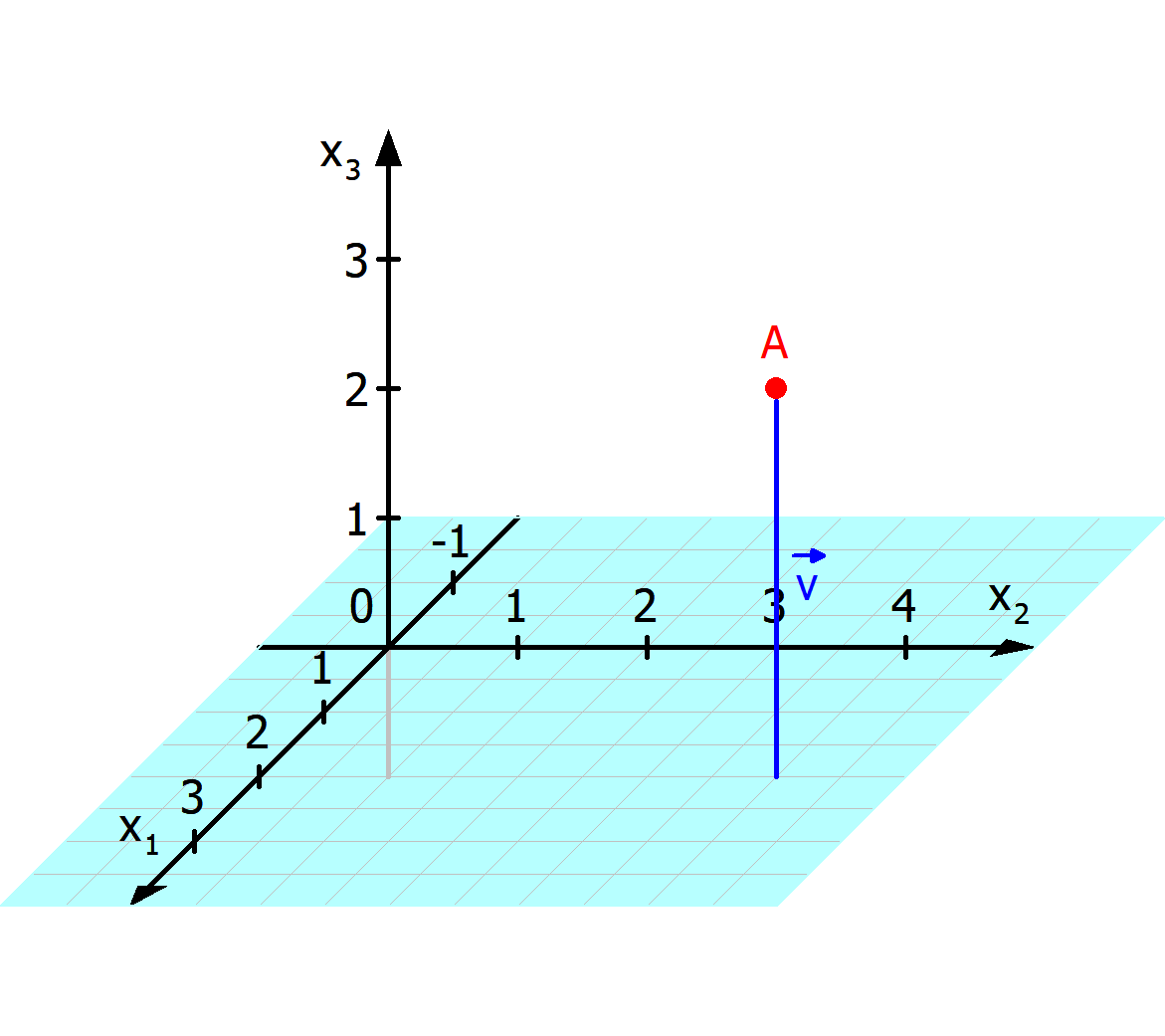
Der Gedanke bei dem Lotfußpunktverfahren ist, das man von dem Punkt $A$, $r$ mal so viele Normalvektoren (der Ebene) nach unten gehen um die Ebene zu treffen. Damit kann man auch schon die "Lotgerade" aufstellen:
$$\begin{align}\vec{l}&=\left(\begin{array}{c} 2 \\ 4 \\ 3 \end{array}\right)+r\cdot \vec{n}\end{align}$$
Nun braucht man aber auch noch den Normalenvektor. Da hier die Ebene in Koordinatenform vorliegt, kann man den Normalenvektor direkt ablesen und in die Lotgerade $\vec{v}$ einfügen:
$$\begin{align}\vec{l}&=\left(\begin{array}{c} 2 \\ 4 \\ 3 \end{array}\right)+r\cdot \left(\begin{array}{c} 0 \\ 0 \\ 1 \end{array}\right)\end{align}$$
Nun kann man einfach ausrechnen, wann sich die Lotgerade und die Ebene treffen:
$$\begin{align}\vec{l}\text{ in }E:\quad 3+r&=0 &&|-3\\r&=-3\end{align}$$
Nun kommt auch endlich der "Lotfußpunkt" ins Spiel. Er markiert einfach nur den Punkt auf der Ebene, welche von der Lotgerade durchbohrt wird. Diesen kann man ausrechnen, in dem man $r$ in die Lotgerade eingibt:
$$\begin{align}r\text{ in }\vec{l}&:\quad\left(\begin{array}{c} 2 \\ 4 \\ 3 \end{array}\right)+(-3)\cdot \left(\begin{array}{c} 0 \\ 0 \\ 1\end{array}\right) \\ \\r\text{ in }\vec{l}&:\quad\left(\begin{array}{c} 2 \\ 4 \\ 0 \end{array}\right)\end{align}$$
Nun kann man sagen der "Lotfußpunkt" liegt bei $P(2|4|0)$. Mit ihm kann man einfach $\overrightarrow{PA}$ berechnen. Denn wenn man den Verbindungsvektor $\overrightarrow{PA}$ kennt, kann man mit dem Betrag des Vektors seine länge und somit den Abstand zwischen der Ebene und dem Punkt errechnen.
$$\begin{align}\vec{v}&=\overrightarrow{PA}=\left(\begin{array}{c} 2 \\ 4 \\ 3 \end{array}\right)-\left(\begin{array}{c} 2 \\ 4 \\ 0\end{array}\right)=\left(\begin{array}{c} 0 \\ 0 \\ 3 \end{array}\right) \\ \\|\vec{v}|&=\sqrt{3^{2}} \\|\vec{v}|&=3\end{align}$$
Das bedeutet der Abstand zwischen dem Punkt $A$ und der Ebene $E$ beträgt 3 Längeneinheiten.
